 “Neural Evolution” (this image was created with the assistance of DALL·E 2)
“Neural Evolution” (this image was created with the assistance of DALL·E 2)
Are you curious about the possibility of evolving artificial neural networks, akin to how biological neural networks have evolved to become more complex over time? In this blog post, I’ll walk you through my implementation of NeuroEvolution of Augmenting Topologies (NEAT), a method proposed by Stanley and Miikkulainen that uses evolutionary principles to guide hyperparameter optimization in neural networks.
Implementing this method from scratch is not only a great exercise but also a fascinating way to explore the potential of evolutionary algorithms in deep learning. To demonstrate NEAT’s ability to model nonlinear data, I’ll use artificial data generated by a simple (noisy) XOR gate as an example.
But before I’m going into the data preparation, let’s get all the library imports done right away. If you are not running this notebook in Google Colaboratory, comment out the lines tagged with Google Colaboratory setting.
%reset -f
from google.colab import drive # Google Colaboratory setting
drive.mount('/content/drive') # Google Colaboratory setting
!pip install gputil # Google Colaboratory setting
import numpy as np
import tensorflow as tf
import random, time, os, copy, sklearn, keras
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.utils import resample
import bokeh, IPython
from ipywidgets import IntProgress
css = open('/content/drive/My Drive/Colab Notebooks/custom.css').read() # Google Colaboratory setting
IPython.display.HTML('<style>{}</style>'.format(css)) # Sets table style
memory = sklearn.externals.joblib.Memory(location='/tmp', verbose=0)
memory.clear(warn=False)
## For reproducible results:
os.environ['PYTHONHASHSEED'] = '3'
random.seed(3)
np.random.seed(3)
tf.set_random_seed(3)
Data Preparation
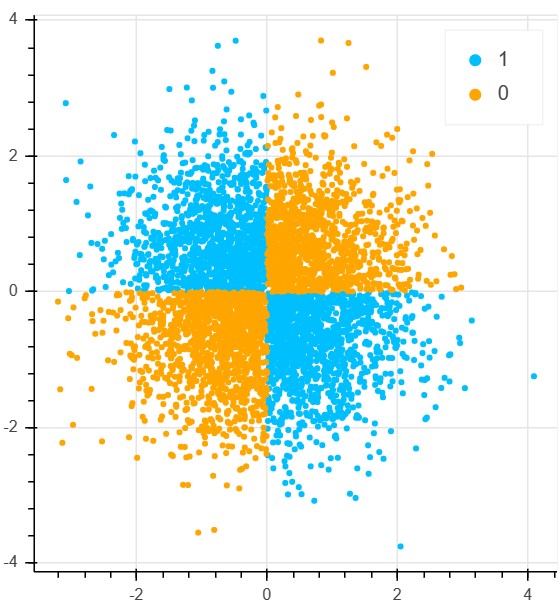
X_xor = np.random.randn(5000, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, 0)
def plot_xor(X, y):
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.models.tools import WheelZoomTool
output_notebook()
p = figure(width=400, height=400)
p.scatter(X[y==1, 0], X[y==1, 1], fill_color='DeepSkyBlue', line_color=None, legend='1')
p.scatter(X[y==0, 0], X[y==0, 1], fill_color='Orange', line_color=None, legend='0')
p.toolbar.active_scroll= p.select_one(WheelZoomTool)
show(p)
return
plot_xor(X_xor, y_xor)
Google Colab provides the opportunity to make use of GPUs and TPUs. With the following code snippet we can see whether a GPU or TPU is used. In case nothing is returned, the CPU will be used. In case you want to use the TPU of google Colab, you have to set the parameter TPU=True in the functions train_standard and neuralNetBuilder. When I last saved this notebook, I used the CPU because it was running 3 times faster with the small models that I am using.
print('Backend: ', tf.keras.backend.backend()) # Return which backend Keras is using
device_name = tf.test.gpu_device_name()
if device_name != '/device:GPU:0':
print('GPU not found')
else:
print('GPU: ', tf.test.gpu_device_name())
import psutil, humanize, GPUtil
GPUs = GPUtil.getGPUs()
for i, gpu in enumerate(GPUs):
print('GPU {:d} ... Mem Free: {:.0f}MB / {:.0f}MB | Utilization {:3.0f}%'.format(i, gpu.memoryFree, gpu.memoryTotal, gpu.memoryUtil*100))
try:
tpu_address = 'grpc://' + os.environ['COLAB_TPU_ADDR']
print('TPU:', tpu_address)
tf.logging.set_verbosity(tf.logging.ERROR)
except KeyError:
print('TPU not found')
This is the output:
Backend: tensorflow
GPU not found
TPU not found
In the following section we prepare the input with standard scaling (actually the XOR dataset is already standardized) and we perform a split of the data into a set for training and a test set which is held back until the very end. Just as a reference, I will set up a minimalistic neural network consisting of 4 hidden units in train_NN. The accuracy is 95% after 10 epochs. Actually, 2 hidden units would also be fine but the number of epochs has to be increased disproportionately. The 4-unit network is a good testing system to figure out some hyperparameters such as activation function or number of epochs.
A quick note regarding the setup: I’m using the TensorFlow backend for Keras. To get GPU support in Google Colab, the only other thing that needs to be done is setting the hardware accelerator in Notebook Settings to GPU. If you want to use Theano, the datatypes have to be converted with something like X_train_test.astype(theano.config.floatX). In addition, when checking the default setting for number datatypes, I first ran into this error message: To use MKL 2018 with Theano you MUST set "MKL_THREADING_LAYER=GNU" in your environement. This can be resolved by running export MKL_THREADING_LAYER=GNU in bash and restarting the notebook. Later, this code can be run on a GPU by executing THEANO_FLAGS=mode=FAST_RUN,device=gpu,floatX=float32 python neural_net.py in bash.
# Preparing Theano input:
def scaleInput(X, y):
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_train_test, y_train_test = X_scaled, y
return X_train_test, y_train_test
def hold_out_split(X, y):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
return X_train, X_test, y_train, y_test
def stratified_ksplit(X, y):
skf = StratifiedKFold(n_splits=10, random_state=3, shuffle=True)
folds = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
folds.append([X_train, X_test, y_train, y_test])
return folds
def transformTPU(model):
tpu_model = tf.contrib.tpu.keras_to_tpu_model(
model,
strategy=tf.contrib.tpu.TPUDistributionStrategy(
tf.contrib.cluster_resolver.TPUClusterResolver(tpu_address)))
return tpu_model
def train_standard(X_train, y_train, epochs, TPU=False):
"""
Training a simple neural network with 4 hidden nodes.
"""
inputs = tf.keras.layers.Input(shape=(2,))
x = tf.keras.layers.Dense(input_dim=X_train.shape[1], units=4,
activation='tanh')(inputs)
y = tf.keras.layers.Dense(1, activation='sigmoid')(x)
model = tf.keras.models.Model(inputs=inputs, outputs=y)
model.compile(loss='mean_squared_error',
metrics=['binary_accuracy'],
optimizer=tf.train.RMSPropOptimizer(learning_rate=0.1))
if TPU:
model = transformTPU(model)
start = time.clock()
model.fit(X_train, y_train, epochs=10, batch_size=64, verbose=0)
end = time.clock()
print('Training completed in %.4f seconds' % (end-start))
return model
X_train_test, y_train_test = scaleInput(X_xor, y_xor)
X_train, X_test, y_train, y_test = hold_out_split(X_train_test, y_train_test)
standard_model = train_standard(X_train, y_train, 10)
standard_model.save_weights('/content/drive/My Drive/Colab Notebooks/standardXORpredictor.h5', overwrite=True)
accuracy = standard_model.evaluate(X_test, y_test, verbose=0)[1]
print('The model achieved an accuracy of %.2f' % accuracy)
Output:
Training completed in 1.2754 seconds
The model achieved an accuracy of 0.93
The following function will display the decision surface of this simple neural network.
def plotDecisionSurface(X, y, model, splitX):
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.models.tools import WheelZoomTool
output_notebook()
grid = np.mgrid[-3:3:100j,-3:3:100j]
grid_2d = grid.reshape(2, -1).T
if splitX:
grid_2d = [grid_2d[:, [i]] for i in range(grid_2d.shape[1])]
prediction_probs = model.predict(grid_2d, verbose=0)
p = figure(x_range=(-5, 5), y_range=(-5, 5), width=400, height=400)
p.image(image=[prediction_probs.reshape(100, 100)], x=-5, y=-5, dw=10, dh=10, palette="Greys9")
p.scatter(X[y==1, 0], X[y==1, 1], fill_color='DeepSkyBlue', line_color=None, legend='1')
p.scatter(X[y==0, 0], X[y==0, 1], fill_color='Orange', line_color=None, legend='0')
p.toolbar.active_scroll= p.select_one(WheelZoomTool)
show(p)
return
plotDecisionSurface(X_train, y_train, standard_model, splitX=False)

From Data Structure to Neural Network Topology
Now that the network was trained in a given parameter configuration, in the next section, I want to change the architecture of the network for better performance. However not by a brute-force gridsearch, but with the least steps possible. To accomplish this task, I will use a genetic algorithm that searches for the best performing neural network architecture. My first attempt at coding a genetic algorithm can be seen in /BasicGeneticAlgorithm/BasicGA.ipynb of this repository.
There, the genetic algorithm was used to evolve a set of binary vectors to finally obtain a uniform vector. However, using a genetic algorithm for the task of evolving a group of neural network architectures is more challenging than using it on binary vectors. First, Stanley and Miikkulainen defined a data structure that contains the “blueprint” of the network topology - the so called genotype. This genotype can then be manipulated by genetic functions. Before manipulating the genotype, however, I want to write a set of functions that can use this “blueprint” to build a neural network.
To give a brief overview of the following code, first groupNetwork goes through the genotype and returns a list with sibling-groups, i.e. nodes of the network which have to be linked. Each of these groups actually contains information about how many nodes are beneath the respective group in the network structure. This allows us to effectively sort the groups from bottom to top with the sortGroups function. neuralNetBuilder can finally translate the sorted list of groups into a compiled neural network.
# Let's say that the genotype (blueprint for neural network) is encoded as follows:
# [ Edge1[InputNode, OutputNode, Weight, Active, InnovationNumber], Edge2[], ...]
example_genotype = [[1, 4, 0.7, 1, 1], [2, 3, 0.2, 1, 4],
[3, 4, 0.2, 1, 4], [1, 3, 0.5, 1, 3]]
def findTop(genotype):
"""
Finds the first of unique output nodes with the most cumulative edges
(see countChildren function). The top node will be the output of the
neural network.
:param genotype: Genotype (blueprint) for building the tree. Shape:
[ Edge1[InputNode, OutputNode, Weight, Active, InnovationNumber], Edge2[], ...]
:type genotype: list
:return: Edge containing the top node as output. An element of
the edges variable.
"""
assert isinstance(genotype, list)
edge_array = np.array(genotype)
unique, indices = np.unique(edge_array[:, [1]], return_index=True) # find unique out_nodes
## Collect active children for each unique output
children_counts = []
for n, u in enumerate(unique):
children_counts.append(countChildren(edge_array, u, 0))
m = max(children_counts)
idx = children_counts.index(m)
top = genotype[indices[idx]]
rank = m # rank = many edges are under the top node
if min(children_counts) < 0:
return top, -1
else:
return top, rank
def countChildren(edge_array, output, cumulative_edges, recursion_counter=0):
"""
Recursive Function that goes through the tree of a neural network and counts
the number of children for a certain output node.
:param edge_array: genotype (blueprint) of the neural network.
:type edge_array: np.ndarray
:param output: Identifier of an output node.
:type output: int
:param cumulative_edges: counter that is incremented whenever a new child is found.
:type cumulative_edges: int
:return: cumulative_edges (int)
"""
a = np.ravel(edge_array[:,[1]]) == output
b = np.ravel(edge_array[:,[3]]) == 1
top_edges = edge_array[np.logical_and(a, b), :].tolist()
count = 0
recursion_counter += 1
if recursion_counter > 200:
return -100000
for i in top_edges:
for e, j in enumerate(edge_array):
if j[1] == i[0] and j[3] == 1:
count += countChildren(edge_array, j[1], 1, recursion_counter)
if count < 0:
return count
return cumulative_edges + count
def findChildren(parent, genotype, edge_idx):
"""
Finds all edges that have the 'parent'-node specified as output.
:param parent: Specifying the edge containing a parent node where
children have to be found.
:type parent: np.array
:param edges: Genotype (blueprint) for building the tree. Shape:
[ Edge1[InputNode, OutputNode, Weight, Active, InnovationNumber], Edge2[], ...]
:type edges: list
:param edge_idx: Keeps track which edges are already part of edge-groups.
:type edge_idx: np.array
:return: List of all children edges connected to that parent node.
"""
children = []
for c, i in enumerate(genotype):
if (i[1] == parent[1]) & (edge_idx[c] == 0):
if i[3] == 1:
children.append(i)
edge_idx[c] = 1
else:
edge_idx[c] = 1 # Make sure that disabled edges don't show up in final network
return children, edge_idx
def groupNetwork(genotype):
"""
Goes through the genotype for building the network and returns a
list with sibling-groups that can be used by neuralNetBuilder().
:param genotype: Genotype (blueprint) for building the tree. Shape:
[ Edge1[InputNode, OutputNode, Weight, Active, InnovationNumber], Edge2[], ...]
:type genotype: list
:return: Sibling groups of edges of edges
"""
assert isinstance(genotype, list)
sibling_groups = [] # Filled from top to bottom
edge_idx = np.zeros(len(genotype)) # To keep track of edges assigned to groups already
count = 0
while len(edge_idx) > 0:
top, rank = findTop(genotype)
if rank < 0:
return None
edge_group, edge_idx = findChildren(top, genotype, edge_idx)
if len(edge_group) > 0:
sibling_groups.append(edge_group + [rank])
mask = copy.deepcopy(edge_idx)
keep = (mask == 0) # Because next round, I want to sort elements that are still unsorted.
keep = np.arange(len(mask))[keep]
genotype, edge_idx = [genotype[i] for i in keep], edge_idx[keep]
count += 1
assert count < 1000, "Problem with the format of genotype:\n%s" % genotype
return sibling_groups
def sortGroups(grouped_network):
"""
Sorting the blueprint of grouped nodes according to the last element within each group.
This last element is an integer that reflects ontop of how many edges the group is built.
Sorting is done in ascending order.
:param grouped_network: List of lists containing the grouped nodes of the genotype.
:return: A sorted list of grouped nodes.
"""
assert isinstance(grouped_network, list)
grouped_network.sort(key=lambda t: t[-1])
# Strip the rank-Value from each element in the list:
sorted_blueprint = [i[:-1] for i in grouped_network]
return sorted_blueprint
def groupToLayer(group, inputs, existing_layers, weights, layercount):
"""
Constructs a layer from a group in the blueprint.
If PReLU layers are switched on (by uncommenting respective lines),
you have to check again the assignment of weights.
:param group: Group element from the blueprint list.
:type group: list
:param inputs: List of Keras Input layer instances.
:param existing_layers: Pass 'None' or a list of existing keras layer
instances in the network.
:param layercount: Tuple containing the current layer level and the
total number of levels. This is used to decide,
when the final layer is reached. The final layer
is constructed differently than the middle layers.
:type layercount: tuple
:return: Keras layer
"""
assert isinstance(group, list)
if existing_layers is not None:
assert len(existing_layers) == len(weights)
# Creating a layer name:
l_name = 'node_' + str(int(group[0][1]))
if existing_layers is None:
if len(group) == 1:
in_node = int(group[0][0]) # Index of input node
if in_node <= len(inputs): # To decide if we use one of the Input instances.
if layercount[0] != layercount[1]: # It's not the final layer
# l = tf.keras.layers.PReLU(input_shape=(1,))(inputs[in_node-1])
l = tf.keras.layers.Dense(1, kernel_initializer='uniform', activation='tanh',
name=l_name)(inputs[in_node-1])
# l = tf.keras.layers.Dense(1, activation='relu', name=l_name)(l)
weights = [group[0][2]]
else: # It's the final layer
l = tf.keras.layers.Dense(1, activation='sigmoid', name=l_name)(inputs[in_node-1])
weights = [group[0][2]]
else:
weights = []
mergelist = []
for j in group:
assert len(j) == 5, "group: %s, edge: %s" % (group, j)
in_node = int(j[0]) # Index of input node
if in_node <= len(inputs):
mergelist.append(inputs[in_node-1])
weights.append(j[2])
if len(mergelist) < 2:
print("There is a problem with the groups %s" % coreBuilder.blueprint)
return None, weights
if layercount[0] != layercount[1]: # It's not the final layer
l = tf.keras.layers.concatenate(mergelist)
# l = tf.keras.layers.PReLU(input_shape=(1,))(l)
l = tf.keras.layers.Dense(1, kernel_initializer='uniform',
activation='tanh', name=l_name)(l)
else: # It's the final layer
l = tf.keras.layers.concatenate(mergelist)
# l = tf.keras.layers.PReLU(input_shape=(1,))(l)
l = tf.keras.layers.Dense(1, activation='sigmoid', name=l_name)(l)
else:
if len(group) == 1:
l = tf.keras.layers.Dense(1, kernel_initializer='uniform',
activation='tanh', name=l_name)(existing_layers[0])
weights.append(group[0][2])
else:
mergelist = existing_layers
for j in group:
assert len(j) == 5, "group: %s, edge: %s" % (group, j)
in_node = int(j[0]) # Index of input node
if in_node <= len(inputs):
mergelist.append(inputs[in_node-1])
weights.append(j[2])
if len(mergelist) < 2:
print("There is a problem with the groups %s" % coreBuilder.blueprint)
return None, weights
if layercount[0] != layercount[1]: # It's not the final layer
l = tf.keras.layers.concatenate(mergelist)
# l = tf.keras.layers.PReLU(input_shape=(1,))(l)
l = tf.keras.layers.Dense(1, kernel_initializer='uniform',
activation='tanh', name=l_name)(l)
else: # It's the final layer
l = tf.keras.layers.concatenate(mergelist)
# l = tf.keras.layers.PReLU(input_shape=(1,))(l)
l = tf.keras.layers.Dense(1, activation='sigmoid', name=l_name)(l)
try: # Prevent building invalid genotype
l
except NameError:
l = None # None will be caught in later functions
return l, weights
def coreBuilder(inputs, sorted_blueprint):
"""
Algorithm to build up a tree-like network topology bottom up from inputs to outputs.
A list of edges (including input, output, weight, ...) serves as blueprint.
:param inputs: List of Keras input layer objects.
:param sorted_blueprint: Output list of sortGroups(). Serves as blueprint
for building the network.
:return layers[-1][0]: From the list of generated layers, from the last element,
the keras model instance.
"""
coreBuilder.blueprint = sorted_blueprint
ngroups = len(sorted_blueprint)-1 # '-1' because it will be matched with n
layers = []
for n, group in enumerate(sorted_blueprint):
if len(group) == 1:
if len(layers) > 0:
outnodes = [int(a[1]) for a in layers]
if int(group[0][0]) in outnodes:
layer_idx = outnodes.index(group[0][0])
l, weights = groupToLayer(group, inputs, [layers[layer_idx][0]], [layers[layer_idx][2]], (n, ngroups))
else:
l, weights = groupToLayer(group, inputs, None, None, (n, ngroups))
else:
l, weights = groupToLayer(group, inputs, None, None, (n, ngroups))
else:
if len(layers) > 0:
outnodes = [int(a[1]) for a in layers]
weights = []
merge_layers = []
for edge in group:
if int(edge[0]) in outnodes:
layer_idx = outnodes.index(int(edge[0]))
merge_layers.append(layers[layer_idx][0])
weights.append(layers[layer_idx][2])
if len(merge_layers) > 0:
l, weights = groupToLayer(group, inputs, merge_layers, weights, (n, ngroups))
else:
l, weights = groupToLayer(group, inputs, None, None, (n, ngroups))
else:
l, weights = groupToLayer(group, inputs, None, None, (n, ngroups))
if l is None:
return None, None
layers.append((l, group[0][1], weights)) # Store tuple ('keras layer', out-node)
return layers[-1][0], layers[-1][2] # Keras instance of the last layer (includes all others).
def setWeightsHelper(l, deep):
sublists = []
if isinstance(l, list):
has_list = 0
for element in l:
if isinstance(element, list):
sublists = setWeightsHelper(element, 1)
has_list = 1
elif deep == 1:
sublists.append([[element]])
return sublists
def setWeights(model, weights):
"""
Goes through the list of weights returned by get_weights and assembles a
new list of numpy arrays based on the edge elements in 'sorted_blueprint'.
:param model: Keras Model instance.
:param sorted_blueprint: List of edges that define the network
(including input, output, weight, ...)
:return: Model instance with adjusted weights.
"""
print(model.get_weights())
sublists = setWeightsHelper(weights, 0)
for n, i in enumerate(weights):
if isinstance(i, list):
weights[n] = 1.0
weights = sublists + [[[i] for i in weights]]
print(weights)
w = []
for i in weights:
w.append(np.array(i, dtype='float32'))
w.append(np.array([0.0], dtype='float32'))
print(w)
model.set_weights(w)
return model
def neuralNetBuilder(X_train, y_train, epochs, sorted_blueprint, TPU=False):
"""
:param X_train: np.ndarray holding the features for training.
:param y_train: np.ndarray holding the outcomes for training.
:param epochs: Integer specifying training iterations over the
entire X and y data.
:param sorted_blueprint: Output list of sortGroups(). Serves as blueprint
for building the network.
:return model: A trained model.
"""
for g in sorted_blueprint:
assert isinstance(g, list), "Problem with the format of sorted_blueprint:\n%s" % sorted_blueprint
for e in g:
assert isinstance(e, list), "Problem with the format of sorted_blueprint:\n%s" % sorted_blueprint
assert len(e) == 5, "Problem with the format of sorted_blueprint:\n%s" % sorted_blueprint
inputs = []
for i in range(X_train.shape[1]):
name = i+1
inputs.append(tf.keras.layers.Input(shape=(1,), name='input_'+str(name)))
main_output, weights = coreBuilder(inputs, sorted_blueprint)
if main_output is None:
return None
model = tf.keras.models.Model(inputs=inputs, outputs=main_output)
model.compile(optimizer=tf.train.RMSPropOptimizer(learning_rate=0.1),
loss='mean_squared_error',
metrics=['binary_accuracy'])
if TPU:
model = transformTPU(model)
in_arrays = [X_train[:, [i]] for i in range(X_train.shape[1])]
# model = setWeights(model, weights)
model.fit(in_arrays, y_train, epochs=epochs, batch_size=64,
validation_split=0.2, verbose=0)
return model
# Then the phenotype for 'example_genotype' looks like:
grouped_network = groupNetwork(example_genotype)
if grouped_network is None:
print('There was probably an infinite loop in the countChildren function')
else:
sorted_blueprint = sortGroups(grouped_network)
trial = neuralNetBuilder(X_train[:, :], y_train, 10, sorted_blueprint)
trial.summary()
IPython.display.SVG(keras.utils.vis_utils.model_to_dot(trial).create(prog='dot', format='svg')) # Display image
# keras.utils.plot_model(trial, to_file='example_network.svg') # Saving the image
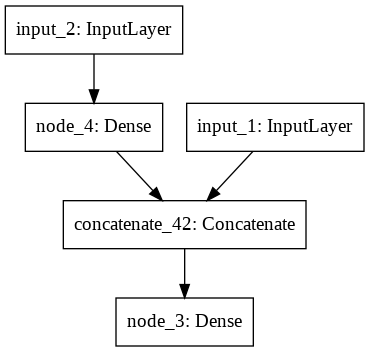
That’s our network architecture:
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_2 (InputLayer) (None, 1) 0
__________________________________________________________________________________________________
input_1 (InputLayer) (None, 1) 0
__________________________________________________________________________________________________
concatenate (Concatenate) (None, 2) 0 input_2[0][0]
input_1[0][0]
__________________________________________________________________________________________________
node_3 (Dense) (None, 1) 3 concatenate[0][0]
__________________________________________________________________________________________________
concatenate_1 (Concatenate) (None, 2) 0 node_3[0][0]
input_1[0][0]
__________________________________________________________________________________________________
node_4 (Dense) (None, 1) 3 concatenate_1[0][0]
==================================================================================================
Total params: 6
Trainable params: 6
Non-trainable params: 0
__________________________________________________________________________________________________
Evolving Neural Network Topologies
As mentioned before, my first genetic algorithm was only able to manipulate a binary vector with genetic operations. I will adapt the algorithm in the next section to properly handle our genotype, i.e. the blueprint for building the neural network topologies.
Here is a quick summary of what will happen in the next part. The geneticAlgorithm function spawns an initial population of 20 individuals from a simple network template (with no hidden units). The 20 individuals are then carried through the 10 generations within the geneticAlgorithm function.
In each generation evolve is called, which performs genetic operations on the population. That means, individuals of the respective generation are ranked according to their fitness, selected for mating with a probability proportional to their rank, and finally the offspring is mutated. Mutation operations can be an insertion of a new hidden node between two linked nodes, or the establishment of a new link between two existing nodes.
innovationCounter = 2
class Individual:
def __init__(self, genotype):
assert isinstance(genotype, list)
self.genotype = genotype
self.epochs = 50
self.phenotype = None
self.disjoint = None
self.excess = None
def build(self, X_train, y_train):
"""
Build and train the network.
"""
self.genotype.sort(key=lambda t: t[-1])
# Groups nodes that have to be merged
grouped_network = groupNetwork(self.genotype)
if grouped_network is None or len(grouped_network) == 0:
# Is None if the network contained circles
# Does not contain elements if all edges were deactivated
return None
else:
# Sorts the node-groups (input towards output).
self.sorted_blueprint = sortGroups(grouped_network)
self.phenotype = neuralNetBuilder(X_train, y_train, self.epochs,
self.sorted_blueprint)
if self.phenotype is None:
return None
return self.phenotype
def fitness(self, X_test, y_test):
"""
:param neuralNet: Trained Classifier.
:type neuralNet: keras or sklearn object
:returns: Scalar test loss
"""
split = [X_test[:, [i]] for i in range(X_test.shape[1])]
accuracy = self.phenotype.evaluate(split, y_test, verbose=0)[1]
return accuracy
def initialPopulation(populationSize, X_data, y_data, template):
"""
The initial population is built from the very simple 'template'-blueprint.
To produce individuals, the array element controlling the weight (idx=2)
will be set randomly.
:param populationSize: Size of the population
:type populationSize: int
:return: List of Individual instances that the population is
composed of.
"""
population = []
X_train_val, y_train_val = resample(X_data, y_data,
random_state=None, replace=True)
X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val,
test_size=0.2)
# For progress bar output:
print('Building initial population.')
f = IntProgress(min=0, max=populationSize)
IPython.display.display(f)
for i in range(populationSize):
blueprint = copy.deepcopy(template)
for j in range(len(template)):
blueprint[j][2] = np.random.random()
c = Individual(blueprint)
model = c.build(X_train, y_train)
population.append(c)
f.value += 1
return population
def rankIndividuals(population, X_test, y_test):
fits = [] # To collect the fitnesses of all individuals
for i, individual in enumerate(population):
fits.append((i, individual.fitness(X_test, y_test)))
fits.sort(key=lambda tup: tup[1], reverse=True)
return np.array(fits)
def selection(rankedPopulation):
"""
Making a selection prior to mating. Individuals are selected with
probability proportional to their fitness.
"""
result = [] # collects the indexes of fittest individuals
max_fitness = np.amax(rankedPopulation[1])
min_fitness = np.amin(rankedPopulation[1])
# To preserve the 20% fittest individuals
for i in range(int(0.2*len(rankedPopulation))):
result.append(int(rankedPopulation[[i], [0]]))
a = rankedPopulation[:, [1]] + 1000000 # 1000000 - because of negative probabilities in some cycles
a_sum = np.sum(np.ravel(a))
probabilities = [i / a_sum for i in a]
probabilities = np.ravel(np.array(probabilities))
theRest = np.random.choice(np.ravel(rankedPopulation[:,[0]]),
int(0.8*len(rankedPopulation)), p=probabilities)
result += [int(i)for i in theRest]
return result
def matingIndividuals(population, selection):
"""
:param population: List of instances of the 'Individual' class from the
previous generation.
:type population: list
:param selection: Result of selection(). Holds the indexes of individuals
for mating.
:type selection: list
:return List of instances of the 'Individual' class, that were
chosen for mating.
"""
pool = []
for i in range(len(selection)):
ind = int(selection[i])
pool.append(population[ind])
return pool
def crossover(parentA, parentB):
"""
This function will align both genomes and look for matching genes. If genes
match, a random gene (parentA or parentB) will be passed to the child
genotype (child_gt). If they don't match, they are either disjoint or
excess. If they are disjoint, their innovation number lies within the
maximum innovation number of the other parent. If they are excess, their
innovation number lies outside the innovation number range of the other
parent. A count for disjoint and excess genes will be accordingly
incremented and passed to the Individual class instances of the parents.
:param parentA: Instance of the Individual class.
:param parentB: Instance of the Individual class.
:return genotype for the child. Instance for parent A and instance
for parent B
"""
child_gtype = []
unique_numbers = [] # Unique innovation numbers
disjoint, excess = 0, 0 # Counters for disjoint and excess genes, passed to the new Individual instance
gtA = parentA.genotype
gtA = np.array(gtA)
gtB = parentB.genotype
gtB = np.array(gtB)
## From the parent genomes, make a new array containing only the innovation numbers:
inno_A = np.ravel(np.array([i[4] for i in gtA.tolist()]))
maxA = np.amax(inno_A)
inno_B = np.ravel(np.array([i[4] for i in gtB.tolist()]))
maxB = np.amax(inno_B)
## Match these arrays and return a boolean array
c = np.in1d(inno_A, inno_B)
for i, test in enumerate(c):
if inno_A[i] not in unique_numbers:
if test: # If innovation number of Parent A gene appears in Parent B
a = np.random.randint(2, size=None) # Decides from which parent the gene will be donated
if a == 1:
condition = np.ravel(gtA[:, [4]] == inno_A[i])
child_gtype.append(np.ravel(gtA[condition, :][0]).tolist())
else:
condition = np.ravel(gtB[:, [4]] == inno_A[i])
child_gtype.append(np.ravel(gtB[condition, :][0]).tolist())
else:
if parentA.fitness(X_test, y_test) > parentB.fitness(X_test, y_test):
child_gtype.append(np.ravel(gtA[[i], :]).tolist())
if inno_A[i] < maxB: # Will be needed for speciation later on
disjoint += 1
else:
excess += 1
unique_numbers.append(inno_A[i])
## Now the same for parentB
c = np.in1d(inno_B, inno_A)
for i, test in enumerate(c):
if inno_B[i] not in unique_numbers:
# All matching genes have already been dealt with in the last for loop.
if not test: # If innovation number in Parent B appears NOT in Parent A
if parentB.fitness(X_test, y_test) > parentA.fitness(X_test, y_test):
child_gtype.append(np.ravel(gtB[[i], :]).tolist())
unique_numbers.append(inno_B[i])
if inno_B[i] < maxA: # Will be needed for speciation later on
disjoint += 1
else:
excess += 1
for i in child_gtype:
assert len(i) == 5
new_child = Individual(child_gtype)
new_child.disjoint, new_child.excess = disjoint, excess
return new_child
def newGeneration(populationSize, pool):
"""
:param pool: result of matingIndividuals(). Holds a list of instances of the
'Individual' class, that were chosen for mating.
:type pool: list
"""
elites = int(0.2*len(pool))
children = []
rest = len(pool) - elites
rand_indexes = np.random.randint(low=0, high=len(pool), size=len(pool))
rand_sample = [pool[i] for i in rand_indexes]
for i in range(elites): # To preserve the 20% fittest individuals to the next generation
children.append(pool[i])
for i in range(rest):
# Making a child:
a = np.random.randint(low=0, high=len(pool))
while a == i :
a = np.random.randint(low=0, high=len(pool))
child = crossover(rand_sample[i], rand_sample[a])
children.append(child)
return children
def correctInnovationCounter(innovation):
"""
:param innovation: Tuple containing the input and output node-number.
"""
global innovationCounter
if not set(innovation).issubset(mutatePopulation.seen):
innovationCounter += 1
innovation_number = innovationCounter
mutatePopulation.uniq.append(innovation + (innovation_number,))
mutatePopulation.seen.add(innovation)
else: # Look up what innovation number has already been assigned
a = np.array(mutatePopulation.uniq)[:, [0, 1]]
idx = a.tolist().index(list(innovation))
innovation_number = mutatePopulation.uniq[idx][2]
return innovation_number
def connectivityGuardian(edge, genotype):
"""
Returns the number of active child and parent edges of 'edge'.
:param edge: The current edge we want to find parents and children for.
:param genotype: List with the same shape as in the 'template' variable.
:return: Tuple containing the number of active parent/child edges.
"""
p, c = 0, 0 # Counter for active parents and children.
for i in genotype:
## Collect active parents
if i[0] == edge[1] and i[3] == 1:
p += 1
## Collect active children
if i[1] == edge[0] and i[3] == 1:
c += 1
return (p, c)
def mutate(individuum, rate):
"""
Alters the genotype of an individuum with a probability of <rate>. Both the
weight of an edge in the network as well as the network itself can be mutated.
Uses the function correctInnovationCounter to keep track of innovations and
assign the correct innovation number.
:param individuum: Instance of the 'Individual' class.
:param rate: Mutation rate, e.g. 0.1
:type rate: float
:return An instance of the 'Individual' class.
"""
genotype = individuum.genotype
for i in range(len(genotype)):
a = np.random.random()
if a <= rate:
genotype[i][2] = np.random.random() # Assigning a new weight to the edge
## The 'add connection' Mutation: connecting two previously unconnected nodes.
a = np.random.random()
if a <= rate:
in_nodes = np.ravel(np.array([i[0] for i in genotype]))
out_nodes = np.ravel(np.array([i[1] for i in genotype]))
connections = np.array([i[:2] for i in genotype])
new_connect = [np.random.choice(in_nodes, size=None),
np.random.choice(out_nodes, size=None)]
whCount = 0
while new_connect in connections.tolist() or new_connect[0] == new_connect[1]:
new_connect = [np.random.choice(in_nodes, size=None),
np.random.choice(out_nodes, size=None)]
whCount += 1
if whCount > 100:
break
if whCount <= 100:
# Register new innovation:
new_innovation = (new_connect[0], new_connect[1])
innovation_number = correctInnovationCounter(new_innovation)
# ... Now build a new gene from it:
ng = [new_connect[0], new_connect[1], 1.0, 1, innovation_number]
genotype.append(ng)
## The 'add node' Mutation: new node placed on existing edge.
a = np.random.random()
if a <= rate:
maxOutNode = max([gene[1] for gene in genotype]) # New node number = maxOutNode + 1
idx = np.random.randint(len(genotype))
geneToMutate = copy.deepcopy(genotype[idx])
genotype[idx][3] = 0 # Set old edge inactive
# Make new edges
new_innovation = (geneToMutate[0], maxOutNode+1)
innovation_number = correctInnovationCounter(new_innovation)
ng1 = [geneToMutate[0], maxOutNode+1, 1.0, 1, innovation_number]
genotype.append(ng1)
new_innovation = (maxOutNode+1, geneToMutate[1])
innovation_number = correctInnovationCounter(new_innovation)
ng2 = [maxOutNode+1, geneToMutate[1], geneToMutate[2], 1, innovation_number]
genotype.append(ng2)
for i in genotype:
assert len(i) == 5
individuum = Individual(genotype)
return individuum
def mutatePopulation(population, rate):
"""
Repeats the mutate() function for the whole population.
:param population: List of instances of the 'Individual' class.
:type population: list
:param rate: Mutation rate, e.g. 0.1
:type rate: float
:return: List of mutated instances of the 'Individual' class.
"""
mutants = []
mutatePopulation.seen = set() # Used to assign correct innovation numbers
mutatePopulation.uniq = [] # within the function correctInnovationCounter
for i in population:
mutants.append(mutate(i, rate))
return mutants
def detectCircles(individuum):
"""
This function calls the findTop function. findTop calls countChildren,
which is a recursive function. That means, if there is a circle, usually
countChildren would fall into an infinite loop and finally abort with the
message maximum recursion depth exceeded. However I prevent this by allowing
only a certain recursion depth before the function returns a negative value.
Consequently, findTop will return a negative value. In such a case, this
function will return negative. In consequence the cleanPopulation function
(which called the detectCircles function) will not append the genotype to
the pool of individuums.
"""
genotype = individuum.genotype
top, rank = findTop(genotype)
if rank < 0:
return -1
else:
return 1
def cleanPopulation(population):
"""
Function deprecated. This is handled when building the networks.
Even though Stanley and Miikkulainen's genotype and crossover procedure is
brilliant, the crossover produces some genotypes which contain circles. That
means nodes that refer to some other node that refers back to the
original node. These genotypes cannot be translated into a valid model by
the neuralNetBuilder function. Thus I am using this function to screen for
invalid genotypes. This function calls the detectCircles function to decide
whether an individuum has a valid genotype (i.e. no circles in their gene map)
and, thus, should be appended to the population pool.
"""
clean_individuals = []
for i in population:
if detectCircles(i) > 0:
clean_individuals.append(i)
else:
print('Individuum killed')
return clean_individuals
def replaceDead(currentPopulation, rate, funerals, valids, X_train, y_train):
"""
Replacing individuums that died with mutated random individuums from
the previous generation.
:param currentPopulation: Instances of the Individual class, all with
compiled models in Individual.phenotype.
:type current Population: list
:param rate: Mutation rate, 0 = no mutations, 1 = always mutate.
:type rate: float
:param X_train: Features of the training dataset.
:type X_train: np.ndarray
:param y_train: Dependent variable of the train dataset.
:param X_test: Features of the test dataset.
:type X_test: np.ndarray
:param y_test: Dependent variable of the test dataset.
:type X_test: np.ndarray
:return: The new generation. A list with instances of
the individual class.
"""
# Replacing dead networks with mutated parents.
fillers = []
for _ in range(funerals):
model = None
crash = 0
while model is None:
individuum = np.random.choice(currentPopulation, size=1,
replace=False).tolist()
mutant = mutatePopulation(individuum, rate)[0]
model = mutant.build(X_train, y_train)
crash += 1
assert crash < 100, "Not able to build new individuum."
fillers.append(mutant)
new_generation = valids + fillers
return new_generation
def evolve(populationSize, currentPopulation, rate, X_train, y_train, X_test, y_test):
"""
Advancing individuums through one generation by ranking their fitness,
mating selected individuums, mutating their genotypes, and finally compiling
the genotype into a network. The function also checks if it was possible to
compile the genotype and remove individuums with did not compile.
:param populationSize: Number of individuums in one generation.
:type populationSize: int
:param currentPopulation: Instances of the Individual class, all with
compiled models in Individual.phenotype.
:type current Population: list
:param rate: Mutation rate, 0 = no mutations, 1 = always mutate.
:type rate: float
:param X_train: Features of the training dataset.
:type X_train: np.ndarray
:param y_train: Dependent variable of the train dataset.
:param X_test: Features of the test dataset.
:type X_test: np.ndarray
:param y_test: Dependent variable of the test dataset.
:type X_test: np.ndarray
:return: The new generation. A list with instances of
the individual class.
"""
rankedPopulation = rankIndividuals(currentPopulation, X_test, y_test) # makes array [indexes, fitness]
sel = selection(rankedPopulation) # makes list [indexes]
sel_individuals = matingIndividuals(currentPopulation, sel) # makes list [Instances of 'Individual']
children = newGeneration(populationSize, sel_individuals) # makes list [Instances of 'Individual']
new_generation = mutatePopulation(children, rate) # makes list [Instances of 'Individual']
# For progress bar output:
f = IntProgress(min=0, max=len(new_generation))
IPython.display.display(f)
for individuum in new_generation:
model = individuum.build(X_train, y_train)
f.value += 1 # For progress bar output:
# Check if all individuums have a valid phenotype
valids = []
funerals = 0
for i in new_generation:
if i.phenotype is None:
print('A little network died.')
funerals += 1
else:
valids.append(i)
if funerals > 0:
new_generation = replaceDead(currentPopulation, rate, funerals,
valids, X_train, y_train)
return new_generation
def geneticAlgorithm(populationSize, generations, rate, X_data, y_data, template):
"""
Advancing individuums through a number of generations. Evolutionary operations
are carried out by the evolve function. This function uses an approach similar
to random forests. While the individual networks are randomized to a certain
degree through mutations, each generation uses a (different) randomized
training data set, drawn from the original data with replacement.
:param populationSize: Number of individuums in one generation.
:type populationSize: int
:param generations: Number of generations.
:type generations: int
:param rate: Range for the mutation rate, e.g. [0.8, 0.02],
where a value of 0 = no mutations, 1 = always mutate.
For this example the mutation rate starts at 0.1 in
the first generation, and decreases linearly to 0.02
in the last generation.
:type rate: list
:param X_data: Features of the training dataset.
:type X_data: np.ndarray
:param y_data: Dependent variable of the training dataset.
:type y_data: np.ndarray
:return: Keras Model of the fittest individuum
"""
population = initialPopulation(populationSize, X_data, y_data, template)
# It's a good idea to anneal the mutation rate:
rate = np.linspace(rate[0], rate[1], generations)
champions = []
for i in range(generations):
print(('\nBuilding Generation ' + str(i + 1) +
' (Mutation rate = %.2f)' + '.') % rate[i])
geneticAlgorithm.genCount = i + 1
X_train_val, y_train_val = resample(X_data, y_data, random_state=None, replace=True)
X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val,
test_size=0.2, random_state=None)
population = evolve(populationSize, population, rate[i], X_train, y_train, X_val, y_val)
bestIndividuumIndex = int(rankIndividuals(population, X_val, y_val)[[0], [0]])
bestModel = population[bestIndividuumIndex].build(X_train, y_train)
split = [X_val[:, [i]] for i in range(X_val.shape[1])]
accuracy = bestModel.evaluate(split, y_val, verbose=0)[1]
print('The best model achieved an accuracy of %.2f' % accuracy)
champions.append((bestModel, accuracy))
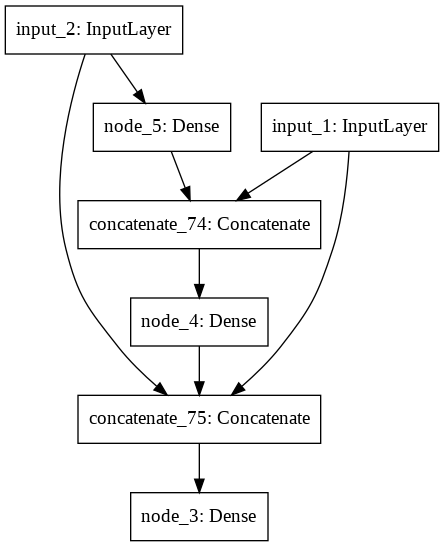
# Produce graphical representation of the architecture:
img = IPython.display.Image(keras.utils.vis_utils.model_to_dot(bestModel).create(prog='dot', format='png'), width=200)
IPython.display.display(img)
champion = sorted(champions, key=lambda x: x[1], reverse=True)[0][0]
return champion
Finally we can execute the geneticAlgorithm function. The following code will also save the weights of the best model and plot its decision surface overlayed with the test set samples.
np.set_printoptions(precision=3, threshold=20) # Used to speed up joblib.
# Defining the template for the initial population:
# shape; [ Edge1[InputNode, OutputNode, Weight, Active, InnovationNumber], Edge2[], ...]
# The number of edges should match the number of features.
template = [[1, 3, 1.0, 1, 1], [2, 3, 1.0, 1, 2]]
start = time.clock()
champion = geneticAlgorithm(populationSize=20, generations=5, rate=[0.8, 0.5],
X_data=X_train, y_data=y_train, template=template)
end = time.clock()
print('Evolution finished in %.1f minutes' % ((end-start)/60.0))
champion.save_weights('/content/drive/My Drive/Colab Notebooks/evolvedXORpredictor.h5', overwrite=True)
print('\nDecision surface of the best model plotted with the test set:')
plotDecisionSurface(X_test, y_test, champion, splitX=True)
X_test = [X_test[:, [i]] for i in range(X_test.shape[1])]
accuracy = champion.evaluate(X_test, y_test, verbose=0)[1]
print('The best model achieved an accuracy of %.2f on the test set.' % accuracy)
Outputs:
Building initial population.
IntProgress(value=0, max=20)
Building Generation 1 (Mutation rate = 0.80).
IntProgress(value=0, max=20)
The best model achieved an accuracy of 0.54
Building Generation 2 (Mutation rate = 0.73).
IntProgress(value=0, max=20)
The best model achieved an accuracy of 0.84
Building Generation 3 (Mutation rate = 0.65).
IntProgress(value=0, max=20)
A little network died.
The best model achieved an accuracy of 0.95
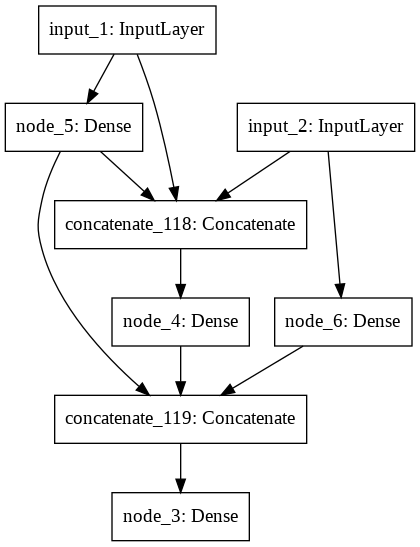
Building Generation 4 (Mutation rate = 0.57).
IntProgress(value=0, max=20)
A little network died.
A little network died.
The best model achieved an accuracy of 1.00
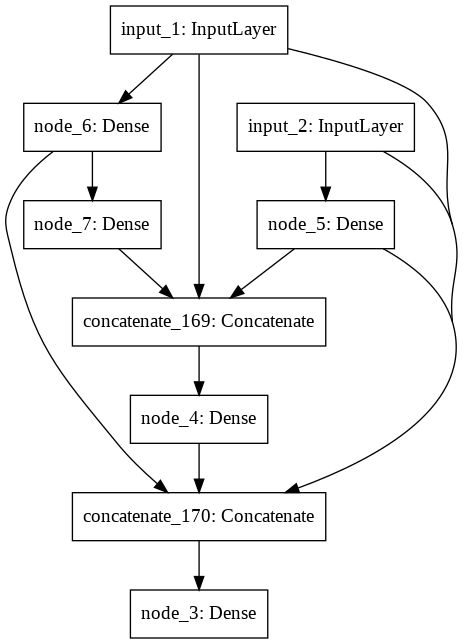
Building Generation 5 (Mutation rate = 0.50).
IntProgress(value=0, max=20)
A little network died.
A little network died.
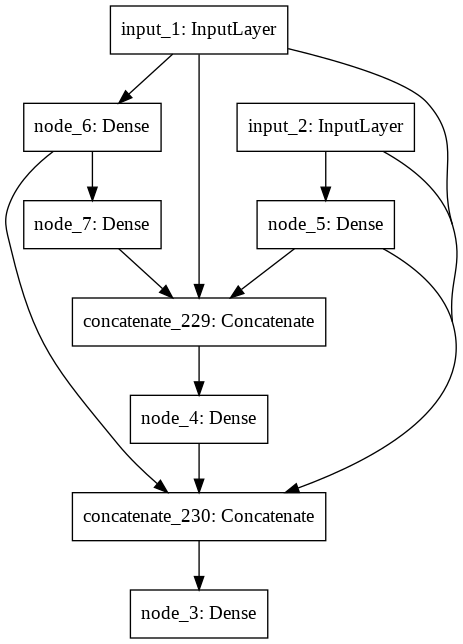
The best model achieved an accuracy of 0.99
Evolution finished in 33.0 minutes
Decision surface of the best model plotted with the test set:
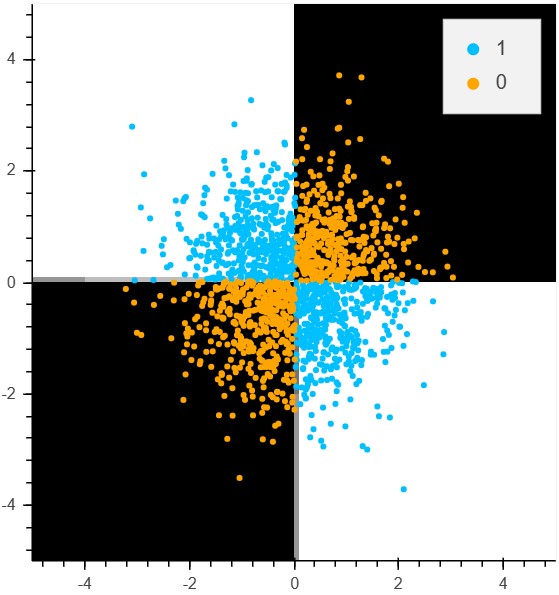
The best model achieved an accuracy of 1.00 on the test set.
Summary and Outlook
The evolution converged within 5 generations to an accuracy of almost 100% in both the validation and the test set. I have repeated the evolution 5 times with different random settings and always got similar results.
So far, there is just one drawback with my code (that I’m aware of). Even though Stanley and Miikkulainen’s genotype and crossover procedure is brilliant, the crossover produces some genotypes which contain circles. By that I mean cases, where node A refers to node B, which refers back to node A. Or node A goes to B then to C, but node C refers back to node A. In principle, these feedback loops would be cool features of this algorithm. But up to now they cannot be handled by my neuralNetBuilder function. In particular they will cause an infinite loop in the countChildren function. The countChildren function can detect such loops and subsequently, the network is dropped from the current population. Thus, whenever you see the output “A little network died.” … that was one of these networks.
A couple of my settings are different from the original NEAT paper. Stanley and Miikkulainen evolved 150 neural networks for an average of 32 generations - I evolved 20 networks for 5 generations. My mutation rate was set to a value of 0.8 (decreasing over time to 0.5) to show the diversity that mutations can introduce into the topologies. The mutation rate in the original paper is 0.3 - still quite high for a genetic algorithm, but the authors say that the system is quite tolerant to high mutation rates because of their speciation procedure. This hits another topic which I want to discuss in more detail.
Speciation is a method to protect new mutations. New mutations tend to get lost because at the time of their inception, they might not provide much of an advantage. However, they may provide an advantage in combination with further developments.
Even without speciation, the code works fine so far on the XOR problem. Speciation might be a critical point though when it comes to more complex problems. The authors of NEAT have also run experiments without speciation. They found that the algorithm failed in 25% of the attempts and was overall 7 times slower. In addition, since structural innovations didn’t survive most of the time, they started out with a population of random topologies (I did not). Despite the additional diversity of starting structures, the population quickly converged to whatever topology performed best in the beginning. To improve speed and failure rate for more complex problems, my next goal will be to add speciation to my algorithm.

